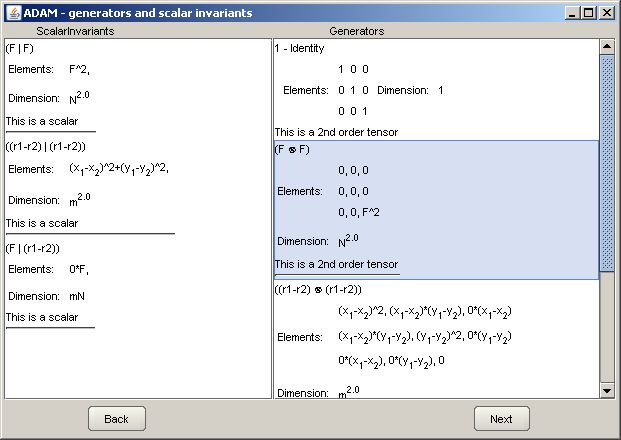
If you succesfully accomplished definition process you can click next in the main window to see some results. On the first window there are lists of scalar invariants (left) and space generators (right). This lists have the form similar to the one we encountered in the quantity definition form i.e. they describe symbol, name, dimension, type and elements of the quantity. These list are read only.

The next section is a bit more complex. On the left you will find a list of dimensional invariants in the current dimensional base. By changing the choice in a combo box above that list you will be able to change a dimensional base for the current generator (generator can also be chosen in the combo box). Note however that your changes will be applied only when you choose the dimensional base.

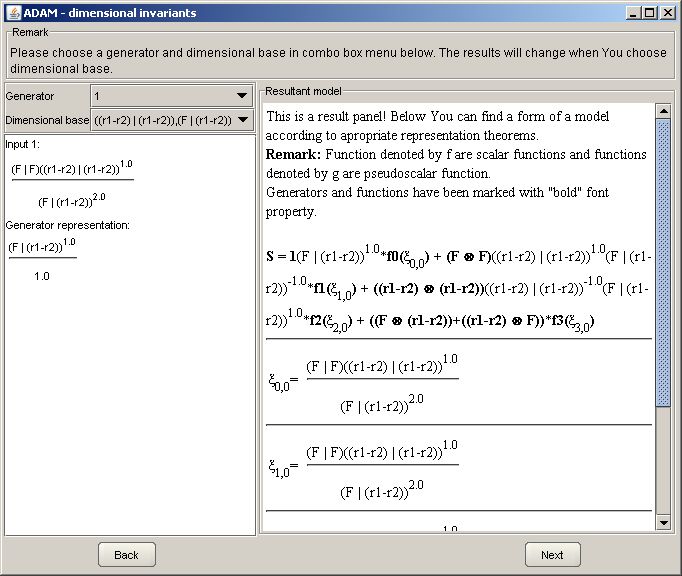
On the right there is a text area which summarizes the result. You will find there the ultimate form of a model, including generators and scalar, dimensional invariants. Wang theorem says that this form is a sum of space generators multiplied by scalar functions. The list of all dimensional invariants for all generators is also included. Now you can change the dimensional bases to express your model in the form that is most suitable for you - the program will automatically recompute all expressions according do your choice. Enjoy!

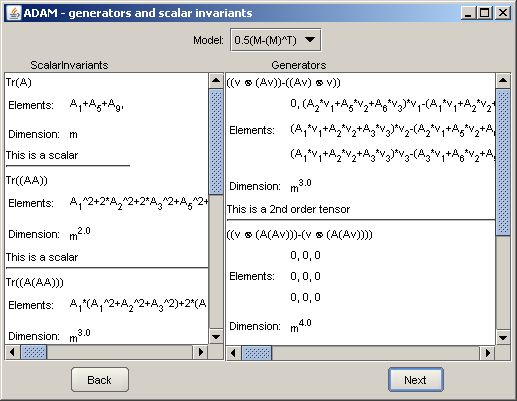
As we have stated before Wang theorems don't say anything about non symmetric matrices i.e. not symmetric or antisymmetric. However any non symmetric matrices can be decomposed into a symmetric and antisymmetric one. Of course ADAM lets you forget about this technical nuisances. Your input quantities will be decomposed into appropriate representations. If an output of your process is a non-symmetrical tensor then an additional combo box will appear in the window with generators and scalar invariants list. This combo box will allow you to choose a part of the process that you want to examine further. You can easily switch between symmetrical and non-symmetrical processes. Remember that your output will be a sum of those symmetric and antisymmetric representations.